Bond order potential
Bond order potential is a class of empirical (analytical) potentials used, e.g., in molecular dynamics and molecular statics simulations. Examples include the Tersoff potential,[1] the Brenner potential,[2] the Finnis-Sinclair potentials [3] and the second-moment tight-binding potentials. [4] They have the advantage over conventional molecular mechanics force fields in that they can, with the same parameters, describe several different bonding states of an atom, and thus to some extent may be able to describe chemical reactions correctly. The potentials were developed partly independently of each other, but share the common idea that the strength of a chemical bond depends on the bonding environment, including the number of bonds and possibly also angles and bond length. It is based on the Linus Pauling bond order concept [1] ,[5] and can be written in the form
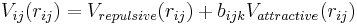
This means that the potential is written as a simple pair potential depending on the distance between two atoms 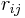 , but the strength of this bond is modified by the environment of the atom i via the
, but the strength of this bond is modified by the environment of the atom i via the 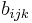 term. Alternatively, the energy can be written in the form
term. Alternatively, the energy can be written in the form
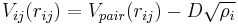
where 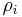 is the electron density at the location of atom i. These two forms for the energy can be shown to be equivalent. [6]
is the electron density at the location of atom i. These two forms for the energy can be shown to be equivalent. [6]
A more detailed summary of how the bond order concept can be motivated by the second-moment approximation of tight binding and both of these functional forms derived from it can be found in [7]
The original bond order potential concept has been developed further to include distinct bond orders for sigma bonds and pi bonds in the so called BOP potentials. .[8]
Extending the analytical expression for the bond order of the sigma bonds to include fourth moments of the exact tight binding bond order reveals contributions from both sigma- and pi- bond integrals between neighboring atoms. These pi-bond contributions to the sigma bond order are responsible to stabilize the asymmetric before the symmetric (2x1) dimerized reconstruction of the Si(100) surface.[9]
Also the ReaxFF potential can be considered a bond order potential, although the motivation of its bond order terms is different from that described here.
References
- ^ a b Tersoff, J. (1988). Phys. Rev. B 37: 6991. Bibcode 1988PhRvB..37.6991T. doi:10.1103/PhysRevB.37.6991.
- ^ Brenner, D. W. (1990). Phys. Rev. B 42 (15): 9458. Bibcode 1990PhRvB..42.9458B. doi:10.1103/PhysRevB.42.9458.
- ^ Finnis, M. W. (1984). "A simple empirical N-body potential for transition metals". Phil. Mag. A 50 (1): 45. Bibcode 1984PMagA..50...45F. doi:10.1080/01418618408244210.
- ^ Cleri, F.; V. Rosato (1993). "Tight-binding potentials for transition metals and alloys". Phys. Rev. B 48: 22. Bibcode 1993PhRvB..48...22C. doi:10.1103/PhysRevB.48.22.
- ^ Abell, G. C. (1985). Phys. Rev. B 31: 6184. Bibcode 1985PhRvB..31.6184A. doi:10.1103/PhysRevB.31.6184.
- ^ Brenner, D. (1989). Phys. Rev. Lett. 63: 1022. Bibcode 1989PhRvL..63.1022B. doi:10.1103/PhysRevLett.63.1022.
- ^ Albe, K.; K. Nordlund (2002). Phys. Rev. B 65: 195124.
- ^ Pettifor, D. G.; I. I. Oleinik (1999). "Analytic bond-order potentials beyond TersofF Brenner. I. Theory". Phys. Rev. B 59: 8487. Bibcode 1999PhRvB..59.8487P. doi:10.1103/PhysRevB.59.8487.
- ^ Kuhlmann, V.; K. Scheerschmidt (2007). "σ-bond expression for an analytic bond-order potential: Including π and on-site terms in the fourth moment". Phys. Rev. B 76 (1): 014306. Bibcode 2007PhRvB..76a4306K. doi:10.1103/PhysRevB.76.014306.